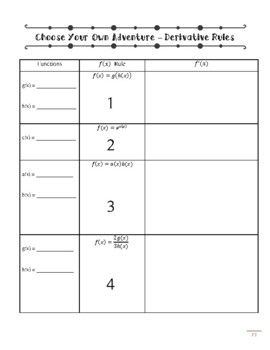
Unit 11 AP Calculus BC Final Exam Review. Unit 3 - Rules of Differentiation.Quiz (Days 1 - 3): Friday, September 29th. Day 3 - Finding the Derivative of a.
- Unit 3 Derivative Rules Of Compositesap Calculus Solver
- Unit 3 Derivative Rules Of Compositesap Calculus 2nd Edition
- Unit 3 Derivative Rules Of Compositesap Calculus Calculator
- Unit 3 Derivative Rules Of Compositesap Calculus Integrals
- Unit 3 Derivative Rules of Composites Watch the video below while filling out Notes. Notes 4 corners key & Video Explanation of Analytical.
- 3 x,a 0 For # 7 – 9, use the definition h f x h f x f x h ( ) ( ) ( ) lim 0 c o to find the general derivative of the function given. F(x) 4x 2 3x 6 9. Find the equations of the line that is tangent and normal to the curve y x 3 at the point (1, 1). If f(2) 3 and fc(2) 5.
You know you’ll have to know your derivatives inside and out in order to score high on the AP Calculus exam. But what are the most common derivatives you’ll see on the test? In this short article, we’ll let you in on the secret!
Know the Basics
First of all, it’s very important to have the basics down. That includes: the Power Rule, Product Rule, Quotient Rule, and Chain Rule, among others.
Acer p223w monitor drivers for mac computer. Don’t forget about those special functions either. You’ll have to memorize the derivative rules for trig, exponential, and logarithmic functions.
Derivatives of trigonometric, exponential, and logarithmic functions
Less common, but no less important are the rules for inverse trig functions.
Best games from last 2 months Categories & more LIBRARY New Games Next in 00:00. Best of new games. Add this game to your web page. This is the best source for free online Bomberman games that you can play on your PC or Mac computers through your web browser. Classic and Unofficial fan games can be found at PlayBombermanOnline.com. Bomberman free flash games online. Play bomberman styled games at Y8.com. Bomberman was one of the first multiplayer games from the original Nintendo console. Ever since then, the gameplay of the Bomberman games have been cloned and remixed to create the same feel of the old games with a little more excitement.
Check out Calculus Review: Derivative Rules and Derivatives on the AP Calculus AB & BC Exams: A Refresher for more.
Common Derivatives
Now let’s take a look at a few problems involving common derivatives that are modeled after actual AP Calculus problems.

Problem 1
Find The tangent line to the curve f(x) = x4 + 3x – 10 at the point (1, -6).
Solution
To find a tangent line, first take the derivative. Here, we have to use the Power Rule and Sum/Difference Rule.
f '(x) = 4x3 + 3
Then you can find the slope and the equation of the tangent line.
Slope at x = 1: f '(1) = 4(1)3 + 3 = 7
y – (-6) = 7(x – 1)
y = 7x – 13.
Problem 2
The position of a particle moving along the x-axis at time t is x(t) = sin( cos( 4t ) ), for 0 ≤ t ≤ π. Find
the velocity at time t = π/8.
Solution
Find velocity by taking the derivative of the position function. Be careful — we need two applications of the Chain Rule for this one!

v(t) = x '(t) = cos( cos( 4t ) ) ( -sin( 4t ) ) (4)
At time t = π/8, the velocity is equal to:
v(π/8) = cos( cos( 4(π/8) ) ) ( -sin( 4(π/8) ) ) (4) = cos( cos( π/2 ) ) ( -sin( π/2 ) ) (4)
= cos(0)(-1)(4) = (1)(-1)(4) = -4.

Problem 3
Find all inflection points of the curve defined by .
Solution
You can find inflection points by taking the second derivative. Of course, you must take the first derivative first. Don’t forget to rewrite your radical as a power and use Chain Rule.
Use Quotient Rule to help find the second derivative.
After simplification, we find that the second derivative is never equal to 0 and never undefined. Therefore this function has no inflection points.
Problem 4
Solution
You’ll need both the Product and Chain Rules for this one.
Problem 5
Suppose g(x) = e4x + 5. At what value of x is the slope of the tangent line to g(x) equal to 3?
Solution
Again, the slope of the tangent line is equal to a derivative value.
g '(x) = 4e4x
Set g '(x) = 3 and solve:
4e4x = 3
Unit 3 Derivative Rules Of Compositesap Calculus Solver
e4x = 3/4
4x = ln(3/4)
x = ln(3/4) / 4 ≈ -0.0719
Summary
Unit 3 Derivative Rules Of Compositesap Calculus 2nd Edition
The five problems above represent just a small sampling of what you’ll find on an AP Calculus AB or BC exam. Nevertheless, the majority of problems involving derivatives do tend to fall into these basic formats.
- Know your basic rules, especially the Chain Rule.
- Memorize the derivatives of the special functions.
- And above all, know which tools apply in each situation.
Good luck on the exam!
Improve your SAT or ACT score, guaranteed. Start your 1 Week Free Trial of Magoosh SAT Prep or your 1 Week Free Trial of Magoosh ACT Prep today!
More from Magoosh
About Shaun Ault
Shaun earned his Ph. D. in mathematics from The Ohio State University in 2008 (Go Bucks!!). He received his BA in Mathematics with a minor in computer science from Oberlin College in 2002. In addition, Shaun earned a B. Mus. from the Oberlin Conservatory in the same year, with a major in music composition. Shaun still loves music -- almost as much as math! -- and he (thinks he) can play piano, guitar, and bass. Shaun has taught and tutored students in mathematics for about a decade, and hopes his experience can help you to succeed!
Unit 3 Derivative Rules Of Compositesap Calculus Calculator
Unit 3 Derivative Rules Of Compositesap Calculus Integrals
Leave a Reply
Magoosh blog comment policy: To create the best experience for our readers, we will approve and respond to comments that are relevant to the article, general enough to be helpful to other students, concise, and well-written! :) If your comment was not approved, it likely did not adhere to these guidelines. If you are a Premium Magoosh student and would like more personalized service, you can use the Help tab on the Magoosh dashboard. Thanks!
